Lecture 2. Double Counting

【定理 1】（握手定理）对 $G=(V,E)$，

推论：图中奇度点的个数一定是偶数。

【证明】可以考虑从关联矩阵考虑，分别对 $|V|\times |E|$ 的关联矩阵的行列计数得到左右两边；也可以对集合 $\{(v,e)\mid v\in e\}$ 计数，即

• 从 $v$ 角度出发，有 $\sum_{v \in V} d(v)$ 个这样的集合；

• 从 $e$ 角度出发，有 $2|E|$ 个这样的集合。

【例 1】证明：

【证明】对第一个等式，即证

考虑 $n$ 个元素的集合 $U=\{1,2,\cdots,n\}$，令 $A\subseteq U$ 且 $|A|=k$，对 $\{(x,A)\mid x\in A\}$ 计数：

• 从 $A$ 角度出发，共有 $\binom{n}{k}$ 个不同的 $A$；对一个固定的 $A$，有 $k$ 个 $x$ 的选择，因此得 $k\binom{n}{k}$；

• 从 $x$ 角度出发，共有 $n$ 个不同的 $x$，对一个固定的 $x$，由于 $x\in A$，因此 $A$ 需要从剩下 $n-1$ 个元素中选出 $k-1$ 个元素，因此有 $\binom{n-1}{k-1}$ 个 $A$ 的选择，得 $n\binom{n-1}{k-1}$。

两边相等，即证明完毕。

对第二个等式。考虑去掉 $|A|=k$ 限制的计数：

• 从 $A$ 角度出发，对每个固定的 $k$，有 $\binom{n}{k}$ 个不同的 $A$；对一个固定的 $A$，有 $k$ 个 $x$ 的选择；因为这里去掉了 $|A|=k$ 的限制，因此需要枚举 $k$ 后求和，即左式；

• 从 $x$ 角度出发，共有 $n$ 个不同的 $x$，对一个固定的 $x$，由于 $x\in A$，因此 $A$ 可以从剩下的 $n-1$ 个元素中任意挑选，因此有 $2^{n-1}$ 个 $A$ 的选择，即右式。

【例 2】令 $0\leq l\leq k\leq n$，证明：

【证明】类似上题，考虑 $n$ 个元素的集合 $U$，令 $A\subseteq U$ 且 $|A|=k$，令 $B\subseteq U$ 且 $|B|=l$，对 $\{(A,B)\mid B\subseteq A\}$ 计数。

• 从 $A$ 角度出发，共有 $\binom{n}{k}$ 个不同的 $A$；对一个固定的 $A$，有 $\binom{k}{l}$ 个不同的 $B$，即得左式；

• 对 $B$ 角度出发，共有 $\binom{n}{l}$ 个不同的 $B$；对一个固定的 $B$，由于 $B\subseteq A$，所以 $A$ 还需要从剩下 $n-l$ 个元素选 $k-l$ 个元素，即有 $\binom{n-l}{k-l}$ 个不同的 $A$，即得右式。

【定理 2】若 $G=(V,E)$ 有 $n$ 个顶点，且不含 4-圈，那么：

【证明】对 $\{(u,(v,w))\mid (u,v)\in E,(u,w)\in E\}$ 计数：

• 从 $u$ 角度出发，
  • 对一个固定的 $u$，$(v,w)$ 的选择有 $\binom{d(u)}{2}$ 种选择方法；
  • 那么总共的集合数量为 $\sum_{u\in V} \binom{d(u)}{2}$ （精确计数）

• 从 $(v,w)$ 角度出发，
  • 对一个固定的 $(v,w)$，最多存在一个 $u$ 满足 $(u,v)\in E, (u,w)\in E$。
    • 若存在 $u_1,u_2$ 均满足上述条件，那么 $u_1,v,u_2,w$ 形成 4-圈，与题目条件矛盾。
  • 有 $\binom{n}{2}$ 个不同的 $(v,w)$ 组合，因此集合数量最多为 $\binom{n}{2}$ （上界计数）

于是，

化简得

于是，代入上述不等式与握手定理，有

即

解一元二次方程即可得到答案。

【例 3】证明在超图 $(V,F)$（边不再是二元集合，可以是多元集合）中，有

【证明】考虑对 $\{(x,A,B)\mid x\in A,x\in B, x\in V,A\in F,B\in F\}$ 计数：

• 从 $x$ 角度出发：
  • 给定 $x$，有 $d(x)$ 个超边 $A$ 包含了 $x$，有 $d(x)$ 个超边 $B$ 包含了 $x$，因此方案为 $d^2(x)$ ；
  • 对 $x$ 求和，得到 $\sum_{x\in X}d^2(x)$。

• 从 $A$ 角度出发：
  • 给定 $A\in F$，由于 $x\in A$，我们从 $A$ 里选择一个点 $x$；
  • 给定 $A\in F,x\in A$，有 $d(x)$ 个超边 $B$ 包含了 $x$；
  • 对 $x$ 求和后对 $A$ 求和，得到 $\sum_{A\in F}\sum_{x\in A} d(x)$。

• 从 $\{A,B\}$ 角度出发：
  • 给定 $\{A,B\}, A,B\in F$，由于 $x\in A,x \in B$，因此有 $|A\cap B|$ 种选择 $x$ 的方案；
  • 对 $\{A,B\}$ 求和，得到 $\sum_{A\in F}\sum_{B\in F} |A\cap B|$。

上述求和应该相等，即证毕。

【定理 3】

【证明】假设我们取出的最少个数的 $l$ 元子集合的集合为 $F$，即 $F=\{Y_1,Y_2,\cdots, Y_{|F|}\}$。令 $Z$ 是一个 $k$ 元子集合，$Y\in F$，对 $\{(Y,Z)\mid Y\subseteq Z\}$ 计数。

• 从 $Y$ 角度出发，
  • 给定一个 $l$ 元子集合 $Y$，由于 $Z$ 必须包括 $Y$，因此 $Z$ 还需要从 $n-l$ 个元素中选出 $k-l$ 个，有 $\binom{n-l}{k-l}$ 种方法；
  • 有 $|F|$ 个 $l$ 元子集合 $Y$，因此得到 $|F|\binom{n-l}{k-l}$ 。

• 从 $Z$ 角度出发，由于每个 $k$ 元子集合至少包括 1 个 $F$ 中的 $l$ 元子集合，因此给定一个 $k$ 元子集合 $Z$，至少有 1 个符合条件的 $(Y,Z)$；共有 $\binom{n}{k}$ 个 $k$ 元子集合，因此得到 $\binom{n}{k}\cdot 1$。

于是，根据双计数有

由于 $T(n,k,l)=|F|$ 且根据【例 2】的结论，有

【双计数的通用表述】给定两个有限集 $R,C$ 以及一个子集合 $S\subseteq R\times C$，当 $(p,q)\in S$ 我们说 $(p,q)$ 是关联的。令 $r_p$ 表示有多少个 $q\in C$ 满足 $(p,q)\in S$；令 $c_q$ 满足有多少个 $p\in R$ 满足 $(p,q)\in S$，那么双计数表示为：

关联矩阵 $A=(a_{pq})_{|R|\times |C|}$ 定义为 $a_{pq}=[(p,q)\in S]$。这样的双计数也可以转化为图论建模：对行列建点，$(p,q)\in S$ 相当于连边，那么可以得到一个（二部）图。

【例 4】令 $t(n)$ 表示 $n$ 的因子数目，那么考虑其算术平均的取值范围。

【解】令 $R=C=\{1,2,\cdots,n\}$，关系为因子关系，那么双计数有

于是，

【例 5】（Zarankiewicz 问题）. 在 $n\times n$ 的 0-1 矩阵中最多能有多少个 1，使其中没有 $a\times b$ 的全 1 子矩阵？

【解】考虑转化为图论建模，变为团的问题。行列建点，成为二分图 $((U,V),E)$；若 $A_{ij}=1$ 则在行节点 $u_i$ 和列节点 $v_j$ 之间连边。那么问题转换为若该二分图没有一个 $a\times b$ 的团 (clique)，最大的边数是多少。

下面考虑 $a=b$ 的情况，$a \ne b$ 情况类似可以证明（但是更加复杂，因此在这略去）。下面的命题给出了 Zarankiewicz 问题的答案。

【命题 1 的证明】考虑对 $(u, \{v_1,v_2,\cdots,v_a\})$ 的结构，其中 $(u,v_i)\in E \ (i=1,2,\cdots,a)$，这些结构的集合记为集合 $S$。对集合 $S$ 进行双计数。

• 从 $\{v_1,v_2,\cdots,v_a\}$ 入手：取定右边的 $a$ 个点，左边最多有 $a-1$ 个点能和 $\{v_1,v_2,\cdots,v_a\}$ 形成此结构（因为不能有 $a\times a$ 的团）；右边的 $a$ 个点有 $\binom{n}{a}$ 个选择。那么，这种估计得到了 $|S|$ 的上界：

  $$|S|\leq (a-1)\binom{n}{a}$$

• 从 $u$ 入手：取定左边的一个点 $u$，有 $\binom{d(u)}{a}$ 个右边点的选择，因此

  $$|S| = \sum_{u\in U}\binom{d(u)}{a}$$

于是，

使用 Jensen 不等式和握手定理，有

于是我们有

考虑右边组合数分子中的的每一项，

同理，左边的组合数有

于是，

两边开 $a$ 次方，有

化简即得，

证毕。

【定理 4】（Sperner 引理）已知平面上的一个三角形 ABC，它被任意划分为若干小的不重叠的三角形。用 $\{1,2,3\}$ 依次对A、B、C三个顶点着色。对其余顶点：BC边上的点用 $\{2,3\}$ 着色；AB上的点用 $\{1,2\}$ 着色；AC边上的点用 $\{1,3\}$ 着色。其他内部顶点任意着色。那么，一定有奇数个三个顶点都不同色的三角形，即顶点染色为 $\{1,2,3\}$ 的三角形，即一定会出现这样的三角形。

【证明 1】每个区域（包括外部剩下的大区域）建立一个顶点；当两个区域公共边的两个顶点染色为 $\{1,2\}$ 时，连接这两个顶点；那么可以构造出出一个图 $G=(V,E)$。假设外部剩下的大区域为点 $x^*$，那么 $x^*$ 一定是一个奇度点（因为其只能与 AB 边上的三角形连边，而 A 和 B 的颜色分别为 1 和 2，且中间点颜色只能从 $\{1,2\}$ 中选择）。

那么，考虑所有染色情况的三角形。我们发现，只有 $\{1,2,3\}$ 三角形，其代表的顶点的度数也是奇数的，其余情况下度数都是偶数的。我们知道，图 $G$ 满足握手定理，即所有点的度数之和为偶数，因此必然有偶数个奇度点，而奇度点的来源只有 (1) 外部点 $x^*$；(2) $\{1,2,3\}$ 三角形，因此必然有奇数个 $\{1,2,3\}$ 三角形，而最小的奇数为 $1>0$，因此一定会出现这样的三角形。

【证明 2】对异色边的数目进行双计数。

• 从边的角度来看，三角形内部的边一定会被计数 2 次，只有 AB、BC、AC 边上的点只会被计数 1 次，由于这些边顶点的特殊染色要求，这些边上的异色边数量一定是奇数。因此，总的异色边数量一定是奇数。

• 从三角形的角度来看，我们发现只有 $\{1,2,3\}$ 三角形有奇数条（3 条）异色边，其余都有偶数条异色边。但我们已经知道，总的异色边数量一定是奇数，那么必然有奇数个 $\{1,2,3\}$ 三角形（因为只有他们能贡献奇数条异色边）。

【例 6】证明

【分析】右边是从 $2n+1$ 个元素中选出 $n$ 个元素的集合的方案数。左边带有求和，与“分类”相关；且带有取整符号，和“奇偶性”相关；有一个 $2^k$ 项，提示考虑“二元集合”。

【证明】考虑 $2n+1$ 个元素 $x_1,x_2,\cdots,x_{2n},x_{2n+1}$；两两分组为

共有 $n$ 个二元组和一个孤立项。那么从这 $2n+1$ 个元素中选出 $n$ 个元素（右边）也可以看成：

1. 从 $n$ 个二元组中取出 $k$ 个二元组，方案数是 $C_n^k$，这些二元组中只能取 1 个元素，其他二元组中必须取 2 个元素或不取元素。

2. 从这 $k$ 个二元组中各取 1 个元素，得到 $k$ 个元素，方案数是 $2^k$；

3. 还剩 $n-k$ 个元素，需要从剩下的 $n-k$ 个二元组和 $x_{2n+1}$ 中挑选；
   1. 考虑 $n-k$ 是偶数，那么一定不能取 $x_{2n+1}$，需要从剩下的 $n-k$ 个二元组中挑选出 $(n-k)/2$ 个二元组，取其中的所有元素；
   2. 考虑 $n-k$ 是奇数，那么一定需要取 $x_{2n+1}$，还需要从剩下的 $n-k$ 个二元组中挑选出 $(n-k-1)/2$ 个二元组，取其中的所有元素；
   3. 综上所述，方案数可以归纳为 $C_{n-k}^{\left[\frac{n-k}{2}\right]}$。

因此，得证。

【例 7】设 $n$ 和 $k$ 是正整数，$S$ 是平面内 $n$ 个点的集合，满足：

1. $S$ 中任何三点不共线；

2. 对 $S$ 中每一点 $p$，至少有 $k$ 个 $S$ 中的点与 $p$ 距离相等。

证明：

【证明】令 $C_j$ 表示以点 $x_j$ 为中心的圆，那么根据 2，必然有 $k$ 个点在 $C_j$ 上。我们可以构造一个“每个点 $x_i$ 是否在 $C_j$ 上”的一个 $n\times n$ 的 0/1 关联矩阵表示这个关系，令 $d(x_i)$ 表示点 $x_i$ 在多少个这样的圆上，也就是矩阵中第 $i$ 行的和，或者关联矩阵表示的图中 $x_i$ 的度数。

那么对考虑 $(x_i,\{C_j,C_k\})$ 计数，其中 $j\ne k$，$x_i$ 在 $C_j$ 和 $C_k$ 上。

• 按照 $x_i$ 计数，那么可以精确计数，共有 $\sum_{i}\binom{d(x_i)}{2}$ 个这样的结构；

• 按照 $\{C_j,C_k\}$ 计数，那么由于两个不同的圆最多有 2 个交点，因此最多有 2 个可能的 $x_i$，从而可以得到计数上界，即最多有 $2\binom{n}{2}$ 个这样的结构。

因此我们得到，

即

根据 Cauchy-Schwarz 不等式，

因此，

$\sum_{i}d(x_i)$ 本身是矩阵的按行计数，因此考虑按列计数，根据 2，每个圆至少有 $k$ 个点，因此

于是，代入原式，转化为

即

于是解得

【例 8】已知集合 $M=(x_1,x_2,\cdots,x_{4n+3})$，它的 $4n+3$ 个子集 $A_1,A_2,\cdots,A_{4n+3}$ 具有如下性质：

1. $M$ 中任意 $n+1$ 个元素恰属于唯一一个子集 $A_j$；

2. $|A_i| \ge 2n+1, \quad i=1,2,\cdots,4n+3$。

证明：任意两个子集 $A_i$ 和 $A_j$ 恰有 $n$ 个公共元。

【证明】考虑构造一个 “每个元素 $x_i$ 是否在集合 $A_j$ 中“ 的一个矩阵；令 $d(x_i)$ 表示 $x_i$ 在多少个集合中，也就是矩阵第 $i$ 行的和。

考虑对 $(x_i,\{A_j,A_k\})$ 结构计数，其中 $j\ne k$，$x_i\in A_j$ 且 $x_i\in A_k$。

• 按照 $x_i$ 计数，那么可以精确计数，共有 $\sum_i \binom{d(x_i)}{2}$ 个这样的结构；

• 按照 $\{A_j,A_k\}$ 计数，那么也可以精确计数，则共有 $\sum_{j,k}^{j\ne k}|A_j\cap A_k|$ 个这样的结构。

因此，

条件 1 保证了对于 $A_j,A_k$，一定有 $|A_j\cap A_k| \leq n$（否则不满足 1），于是

下面考虑证明 (*) 式：

根据 Cauchy-Schwarz 不等式，若满足下面条件则 (*) 式成立：

$\sum_{i}d(x_i)$ 本身是矩阵的按行计数，因此考虑按列计数，根据条件 2 有

那么，只需要证明下面条件则 (*) 式成立：

化简后有

对 $n\ge 0$ 显然成立，因此 (*) 式成立，于是得证。

【例 9】能否把 1, 1, 2, 2, 3, 3, ……, 1986, 1986 这些数排成一行，使得两个 1 之间夹着 1 个数，两个 2 之间夹着 2 个数，两个 1986 之间夹着 1986 个数？

【证明】假设可以，则设第一个 $i$ 排在的位置是 $A_i$，那么第二个 $i$ 排在的位置应该是 $A_i+i$。

那么，$A_1, A_1+1, A_2,A_2+2,\cdots,A_{1986},A_{1986}+1986$ 应该构成 $1,\cdots, 3972$ 的一个排列。两边求和，有

发现，$\frac{1987\cdot 1986}{2}$ 是奇数而 $\frac{3973\cdot 3972}{2}$ 是偶数，由于 $2\sum_{i=1}^{1986}A_i$ 也只能是偶数，因此等式不可能成立，假设不成立。不存在这样的排列。

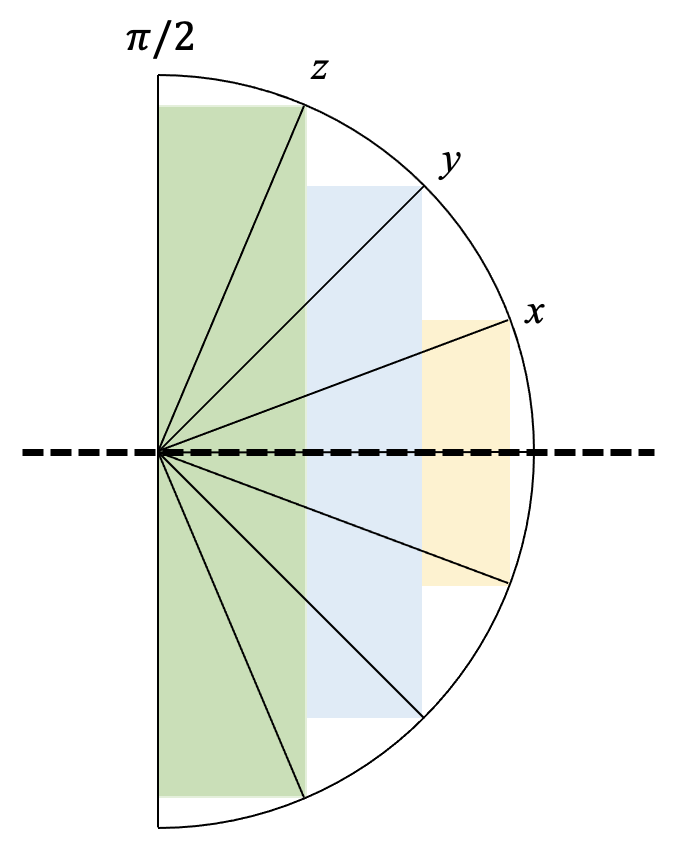
【例 10】设 $x,y,z$ 为实数，并且 $0<x<y<z<\pi/2$，求证：

【证明】

即证：

• $2\sin x(\cos x - \cos y)$：黄色区域的面积；

• $2\sin y (\cos y - \cos z)$：蓝色区域的面积；

• $2\sin z \cos z$：绿色区域的面积；

• $\frac{\pi}{2}$：整个半圆的面积

显然不等式成立。

【例 11】某次会议中有 30 名议员，每两位议员或为政敌或为朋友，而且每位议员都恰有 6 个政敌。对于 3 个议员组成的委员会，若这 3 人中任何两个人都是朋友或任何两个人都是政敌，则称之为奇异委员会。问：共有多少个奇异委员会？

【解】考虑建模成图 $G=(V,E)$，议员为点，关系为边。将政敌关系的边染为黑色，朋友关系的边染为白色。那么奇异委员会即为全黑/全白三角形。那么每个点连出 6 条黑边，23 条白边。那么图中共有 2 类三角形：同色三角形和异色三角形。奇异委员会即为同色三角形，假设有 $x$ 个同色三角形，那么有 $\binom{30}{3}-x$ 个异色三角形。那么对同色角（同色边的夹角）进行双计数。

• 从三角形的角度来说，每个同色三角形有 3 个同色角，每个异色三角形有 1 个同色角，因此总共有 $3x + (\binom{30}{3}-x) = \binom{30}{3} + 2x$ 个同色角。

• 从点的角度来说，每个点连出 6 条黑边与 23 条白边，那么每个点共有 $\binom{6}{2}+\binom{23}{2}$ 个同色角，因此总共有 $30(\binom{6}{2}+\binom{23}{2})$ 个同色角。