Lecture 1. Basic Concepts of Graph

【例 1】某个图具有 $n\ge 8$ 个顶点，试问：这些顶点的度数可否分别为 $4, 5, 6, \cdots, n-4, n-3, n-2, n-2, n-2, n-1, n-1, n-1$？

【解】当 $n=8$ 时，即需要构造出度数为 $4,5,6,6,6,7,7,7$ 的图：

• 考虑三个度数为 7 的点 $x_1,x_2,x_3$，需要和所有其他点相连；

• 考虑三个度数为 6 的点 $x_4,x_5,x_6$，假设他们之间互相相连，那么至少需要与 $x_7,x_8$ 其一相连，而 $x_7,x_8$ 度数分别为 5, 4，于是可以令 $x_4,x_5$ 与 $x_7$ 相连，$x_6$ 与 $x_8$ 相连，即满足条件。

当 $n=9$ 时，在上述构造上继续构造，需要构造出度数为 $4,5,6,7,7,7,8,8,8$ 的图：考虑在上面构造的图中加入一个点 $x_9$：

• 令 $x_9$ 和 $x_1,x_2,x_3$ 均相连，那么这三个点度数变为 8；

• 令 $x_9$ 和 $x_4,x_5,x_6$ 均相连，那么这三个点的度数变为 7；

• $x_9$ 自己的度数为 6，且 $x_7,x_8$ 的度数保持不变，分别为 5,4，满足条件。

但是我们发现 $n=10$ 时不满足条件，下面我们证明 $n\ge 10$ 均无法构造。对于任意 $n\ge 10$，度数序列为 $4, 5, 6, \cdots, n-4, n-3, n-2, n-2, n-2, n-1, n-1, n-1$，分为三部分：

• 第一部分的点必须和其他点全部相连（确定的构造），于是第二部分和第三部分每个点都需要给第一部分的点提供 3 度。

• 第二部分的点除和第一部分的 3 个点相连外，在第二部分内部最多解决 2 个点，因此至少需在第三部分的 $n-6$ 个点中连 $n-7$ 个点；于是第三部分至少需给第二部分提供 $3(n-7)$ 度。

• 考虑第三部分点，给第一部分点提供 3 度后，剩余可用度数为 $1,2,3,\cdots,n-6$，最多可以给第二部分的点提供的度数为：

  $$1+2+\underbrace{3+\cdots+3}_{n-8\text{ 个}}=3(n-7)$$

  到这里我们发现，至少提供 = 最多提供，因此必须刚好提供 $3(n-7)$ 个点，也就意味着第三部分中剩余可用度数为 $1,2,3$ 的点必须把这些度数全部提供给第二部分点。于是，提供给第二部分点后度数变为 $0,0,0,1,2,\cdots,n-9$；这些度数必须在第三部分内部自行解决。但是我们发现，剩余度数为 $n-9$ 的点在第三部分内最多只能连除自己外的剩下 $n-10$ 个度数非 0 的点，导出矛盾。

综上，对于 $n\ge 10$，均无法进行构造。

【例 2】有 5 个工作 $J_1,J_2,\cdots,J_5$，每个工作招聘一名员工；有 7 个应聘者 $A_1,A_2,\cdots,A_7$，应聘者和工作之间连边表示应聘者可以胜任该工作。问题：这 5 个工作能否找到 5 个可以胜任工作的应聘者：

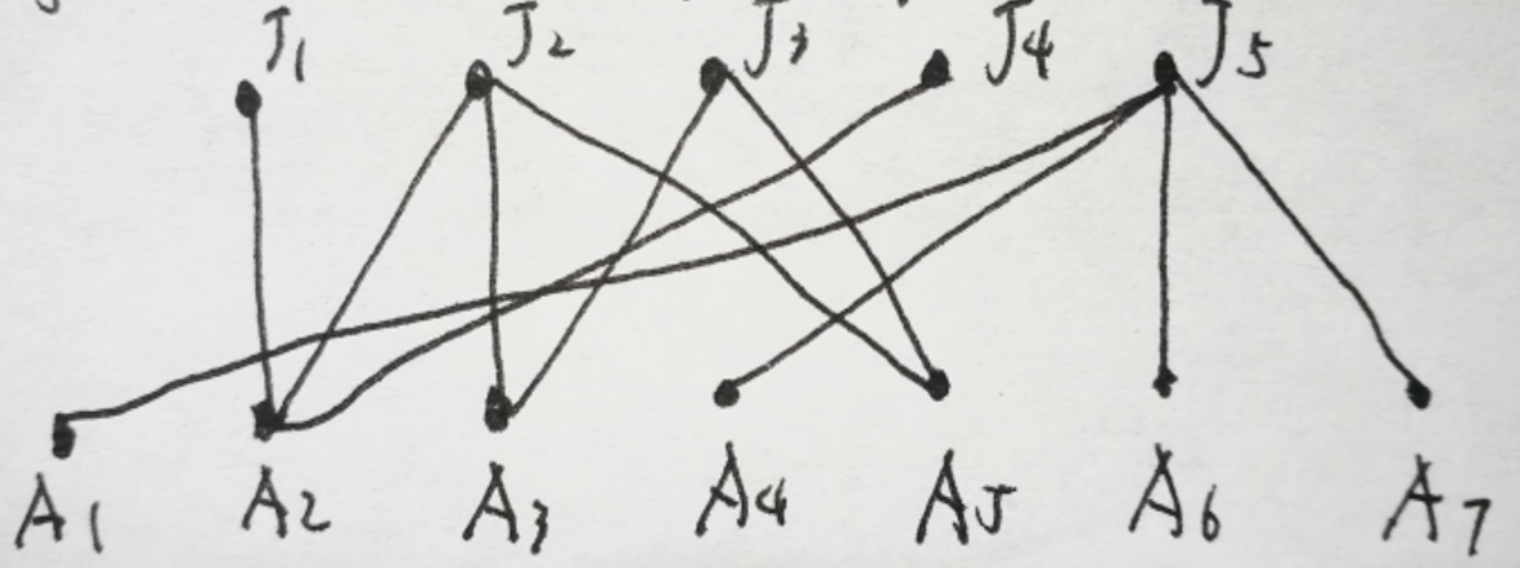
【解】相当于二部图匹配问题，问最大匹配是多少。

【例 3】有 7 种不同的化学品 $C_1,C_2,\cdots,C_7$，因为安全原因，某些化学品 $(C_i,C_j)$ 不能存在同一仓库，为安全地存储这些化学物品，最少需要建多少仓库？

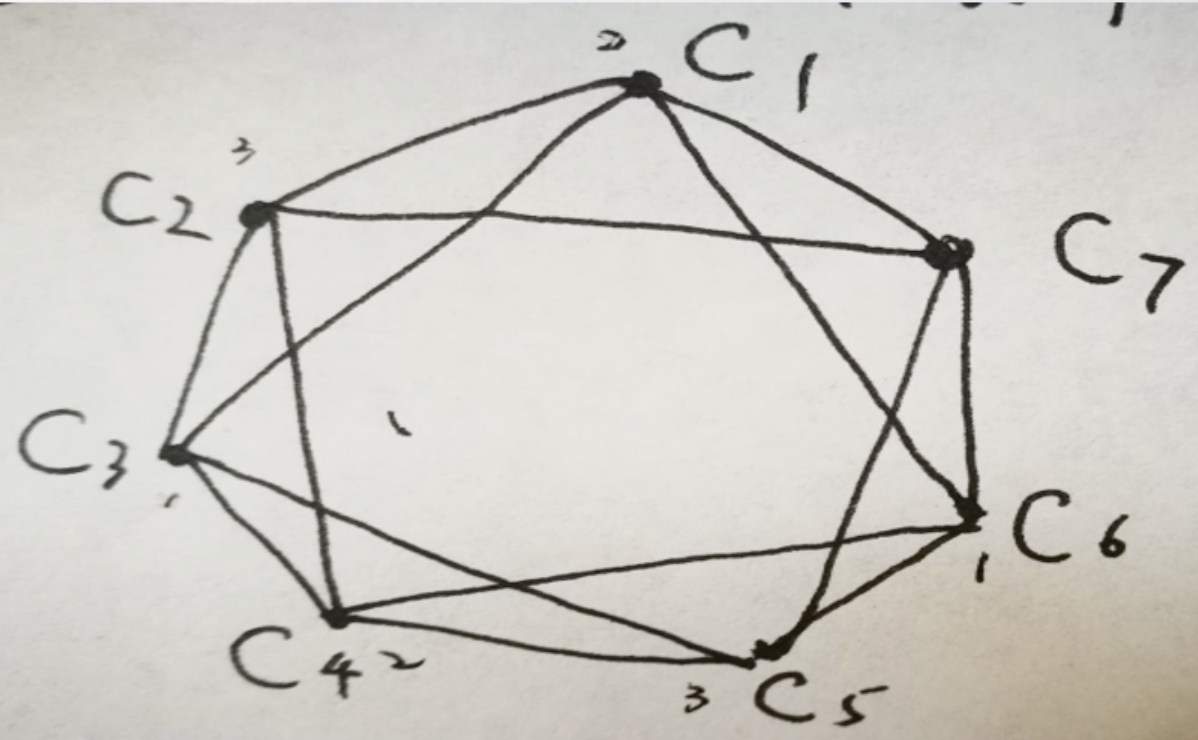
【解】相当于图的色数（用最少的颜色进行染色）。